nonogram安卓版

nonogram安卓版是一款操作簡(jiǎn)單好上手的休閑闖關(guān)游戲，玩家可以通過這款游戲來訓(xùn)練自己的大腦，適合多個(gè)年齡段的玩家，輕松趣味的游戲氛圍讓人愛不釋手，還有舒緩的音樂與音效加入，值得你來嘗試，擁有超多的關(guān)卡，每一個(gè)的設(shè)定都不一樣，很是好玩。

nonogram安卓版玩法

1、縱橫數(shù)字和文字游戲都很好用，你很熟悉，游戲玩法很上癮

2、多種主題拼圖等待您去挑戰(zhàn)，不要忘了領(lǐng)取成就獎(jiǎng)勵(lì)

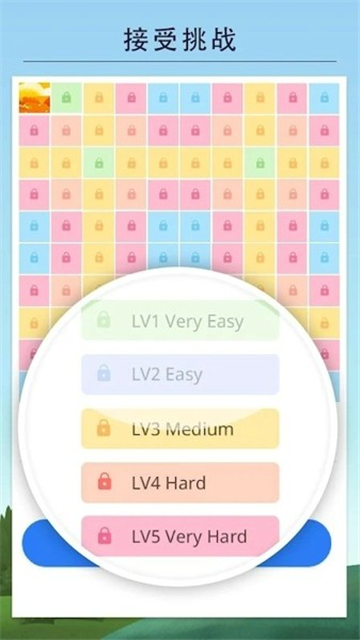
3、5種挑戰(zhàn)模式，選擇最適合您的數(shù)織游戲難度等級(jí)

4、輕松愉快的背景音樂，能使自己快速放松下來

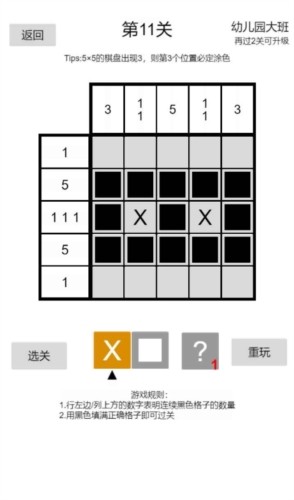
nonogram安卓版優(yōu)勢(shì)

5種挑戰(zhàn)模式，選擇最適合您的數(shù)織游戲難度等級(jí)。

輕松愉快的背景音樂，能使自己快速放松下來。

多種主題拼圖等待您去挑戰(zhàn)。不要忘了領(lǐng)取成就獎(jiǎng)勵(lì)。

簡(jiǎn)單輕松的游戲世界，我們的游戲?qū)W起來容易，玩起來容易，但是很難掌握。

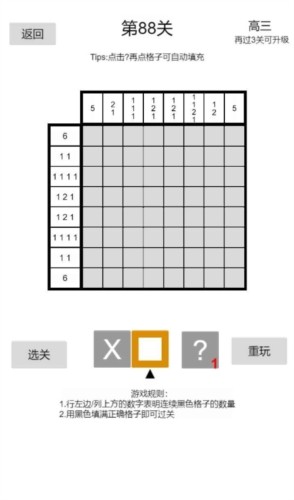
nonogram安卓版新手攻略

本系列中的簡(jiǎn)稱及其說明

1、排：行/列

2、垂直：與排的方向垂直。

3、從k排開始的m×n區(qū)塊：未特指時(shí)，通常指游戲中的所有排的集合。也可以表示一個(gè)矩形的范圍，其中，m表示行，n表示列。

4、場(chǎng)地格：初始狀態(tài)的格子，存在在游戲的區(qū)塊中。

5、第x行格：從任意一邊開始數(shù)的第x個(gè)場(chǎng)地格

6、第x個(gè)數(shù)字：從任意一邊開始數(shù)第x個(gè)數(shù)字

7、數(shù)字x的正格：一定有黑塊的格子，且該場(chǎng)地格一定為數(shù)字x的圖形的一部分

8、負(fù)格：一定無黑塊的格子

9、數(shù)字x的位：數(shù)字x所可能代表的場(chǎng)地格

第一章：數(shù)字的位與數(shù)字的位的確定化

1-1概述

在數(shù)織的過程中，我們就是在與一些模糊的位置打交道，通過這些位置還有區(qū)塊相互間的關(guān)系，我們可以將他們中一部分的準(zhǔn)確位置確定，最終成功推演出整個(gè)圖像。

數(shù)字的準(zhǔn)確位置一般可以由一排的格數(shù)和數(shù)字推出，有時(shí)也需要用到已經(jīng)確定的正格與負(fù)格，只有極少數(shù)的關(guān)卡需要同時(shí)用到兩排以上的信息。這也使得其的難度不是那么的高，本系列致力于幫您從剛?cè)腴T的新手迅速成為能推理大多數(shù)圖形的高玩。

注：以下所有定理與方法中我們將把負(fù)數(shù)看為零。

1-2 推演基礎(chǔ)

如何才能通過推演確定準(zhǔn)確位置?我們可以先提出一條十分簡(jiǎn)單的定理。

若一排有且僅有一個(gè)數(shù)字，則這個(gè)不是數(shù)字的位的場(chǎng)地格均為負(fù)格。(1-2-1)

這條定理不證自明，也可以說是數(shù)字的位定義的另一種表達(dá)。

由這條公理，我們可以看出，確定一個(gè)數(shù)字的準(zhǔn)確位置，就是使其的位減少到無法再減少為止。而交叉的排與單排的限制可以幫助我們減少數(shù)字的位。

我們來看一個(gè)簡(jiǎn)單的例子。

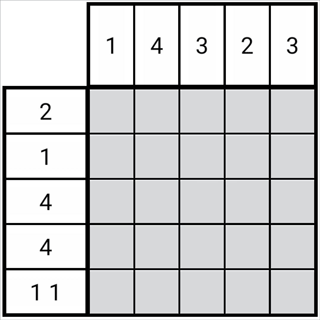
圖1-2-1

如圖所示，每一排的黑塊在規(guī)則下都有有限種分布情況，這些分布情況稱為分布可能。

圖中第二列共有兩種分布可能，而兩種分布可能中有一些公共部分，可以看出，這個(gè)公共部分中的格子一定是正格。

同理，圖中第三列共有三種分布可能，這三種分布可能中也有公共部分，即第三列第三格。于是這個(gè)格子一定也為正格。

更一般的，在一排的所有分布可能中，恒有黑塊的格子為正格。

如果一個(gè)排有一個(gè)正格且只有一個(gè)數(shù)字，我們可以把他看做“固定住”這個(gè)數(shù)字的位的“釘子”，而位可以在其左右“波動(dòng)”，或者說增加格數(shù)，從而得出所有的分布可能。

同時(shí)，當(dāng)有兩個(gè)正格固定住一個(gè)數(shù)字的位時(shí)，其中間的部分也就確定下來一定是正格了。我們也可以用數(shù)學(xué)的語言來將其轉(zhuǎn)換為如下表述：

若一排有且僅有一個(gè)數(shù)字，且確定了第m行格與第n行格均為正格，則第i行格為正格。其中，i∈{x∈N+|m≤x≤n或n≤x≤m}。(1-2-2)

然而，因?yàn)閿?shù)字的大小關(guān)系，一個(gè)數(shù)字的位在正格的兩邊增加一定數(shù)量的格數(shù)。不能超過數(shù)字所規(guī)定的范圍，我們從數(shù)學(xué)角度對(duì)其進(jìn)行推導(dǎo)。

設(shè)一排有且僅有一個(gè)數(shù)字k，第m行格與第n行格為已知正格，且m≧n。由式1-2-2，可知其中間所有格均為正格，總共占去(m-n+1)格。于是，位在左右能增加的格數(shù)為k-(m-n+1)。所以，從兩端增加這么多的格數(shù)即可得到所有的位。既，從第n-[k-(m-n+1)]行格到第m+[k-(m-n+1)]都為該數(shù)字的位。整理后可得：

若一排有且僅有一個(gè)數(shù)字k，且第m行格和第n行格都為正格，則該數(shù)字的位為第(-k+m+1)行格到第(k+n-1)行格。(m≧n)(1-2-2)

1-3邊緣法

我們?cè)谏厦嫣岬剑瑪?shù)字能夠限制位，其實(shí)，還有一種東西能夠限制位。那就是場(chǎng)地格的邊緣。場(chǎng)地格的邊緣以外顯然不能存在位，尤其是第一個(gè)數(shù)字，其必然最接近場(chǎng)地格的邊緣，所以很容易被限制。所以，我們有必要討論邊緣的情況。

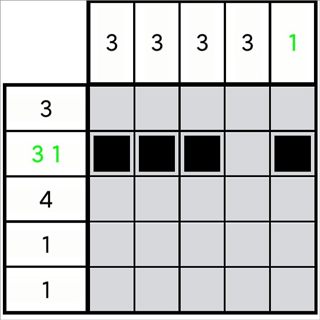
圖1-3-1

如圖1-3-1，顯然，圖中第1列的位不能向上增加兩格，然而其確實(shí)滿足定理(1-2-3)的前置條件。我們可以換一種思考方式，如果不能向上增加，則一定要向下增加。因此，向上不能增加多少格，向下就要增加多少格。

設(shè)一排有且僅有一個(gè)數(shù)字m，且已知第n行格為正格，其中m>n。則其無法增加的格數(shù)為(m-n)格。將這些格數(shù)向下增加，則可以得到：

若一排有且僅有一個(gè)數(shù)字m，且第n行格為正格，m>n，則第i行格為正格，i∈[n，m]，i∈N+。(1-3-1)

觀察該定理，當(dāng)m>n時(shí)，就意味這該數(shù)字代表的位一定覆蓋了第1行格到第n行格。如果我們假設(shè)其為第一個(gè)數(shù)字，那么可以想到，這個(gè)定理依然成立。于是有：

若一排第n行格為正格，且第一個(gè)數(shù)字為m，則第i行格為正格，其中，i∈[n，m]，i∈N+。(m>n)(1-3-2)

當(dāng)一個(gè)數(shù)字在邊緣時(shí)，其狀態(tài)并沒有太多的變化，但是，如果我們討論一整排的情況，又會(huì)如何?

這里我們引入一種方法：整體法，當(dāng)確定兩個(gè)相鄰數(shù)字的位時(shí)，我們可將這兩個(gè)數(shù)字當(dāng)看做一個(gè)數(shù)字處理，他們的位看做這個(gè)數(shù)字的位。這種處理方法可以簡(jiǎn)化我們的運(yùn)算以及幫助我們分析一整排的情況。

我們可以注意到一個(gè)事實(shí)——多個(gè)數(shù)字組成的整體處在邊緣處時(shí)有種獨(dú)特的分布——數(shù)字-空格-數(shù)字-空格。這種分布把數(shù)字占用的空間壓縮為了最小，我們把這種整體在邊緣的分布稱為邊緣狀態(tài)。

如果一個(gè)實(shí)心物體在一條直道內(nèi)滑動(dòng)，可以想象，其投影與初始時(shí)投影公共部分的大小將不斷減少，因此，公共部分其所有運(yùn)動(dòng)瞬間投影的公共部分與其邊緣狀態(tài)的公共部分相同。由此，我們可以得出：

沒有負(fù)格的一排的所有分布可能的公共部分由其邊緣狀態(tài)決定。

可以看出，這種描述看似十分完美，實(shí)際上有一點(diǎn)瑕疵，那就是作為一個(gè)整體，多個(gè)數(shù)字占用的空間可以拉長(zhǎng)和縮短，而邊緣狀態(tài)一定是最短的。但確實(shí)，我們就差一步就能完善它了。

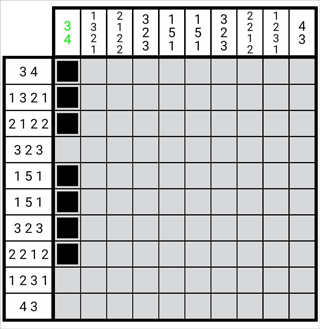
圖1-3-2

如圖，我們可以在第一列從上向下構(gòu)造一個(gè)圖形，其為第一列所有數(shù)字整體的邊緣狀態(tài)，這時(shí)，這一列從下向上數(shù)共有2個(gè)空格。這意味著這個(gè)圖形每個(gè)數(shù)字的位都可以向下增加兩格，于是我們將圖形中對(duì)應(yīng)每個(gè)數(shù)字的圖形從上至下減去兩格，如圖所示。

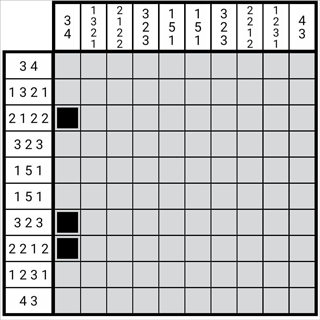
圖1-3-3

這樣我們就得到了這一列的正格。這種方法得出的最終圖形是與原來圖形的數(shù)字位相對(duì)應(yīng)的。這里我們省略了邊緣狀態(tài)的檢查。邊緣狀態(tài)的重疊不重要，重要的數(shù)字與圖形必須一一對(duì)應(yīng)。因?yàn)檫@個(gè)圖形可以變長(zhǎng)變短，但是其中任意一個(gè)圖形活動(dòng)的范圍是有限的，其限制正好就是他自身與區(qū)塊的長(zhǎng)度。只有當(dāng)圖形與數(shù)字一一對(duì)應(yīng)時(shí)這種方法才有意義。由此，我們也反推出了為何其必然一一對(duì)應(yīng)，也可以將該性質(zhì)運(yùn)用在解題中。這也是為第二章的一些鋪墊。

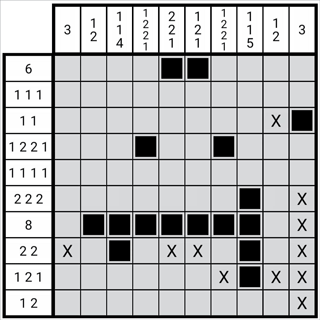
圖1-3-4

如圖，圖中第七列第七行為用此方法確定的第七列第3個(gè)數(shù)字2，由于位置關(guān)系的對(duì)應(yīng)，第4個(gè)數(shù)字1的位一定是第七列第十行。

由上，我們可以總結(jié)一種快速的確定正格的方法：先從一排從第一行格按順序做出如上的數(shù)字-空格圖形，再從開始的方向減去最后剩下的空格數(shù)，將負(fù)數(shù)看為零。最后得到的圖形一定為正格。同時(shí)這些圖形也與原來圖形中的位置關(guān)系相對(duì)應(yīng)，也是運(yùn)用第一章所有方法所能得到的最多正格，這種方法被稱為邊緣法。

nonogram安卓版優(yōu)勢(shì)

1、選擇最適合自己的難度，從零開始逐漸來升級(jí)游戲中的難度;

2、利用像素化邏輯謎題中來找到更多的線索，揭開其中隱藏的圖像;

3、這款縱橫數(shù)字游戲容易上手，開始玩之后會(huì)十分上癮;

4、安靜的背景音樂，各種來自大自然的聲音，很快的使內(nèi)心得以平靜。

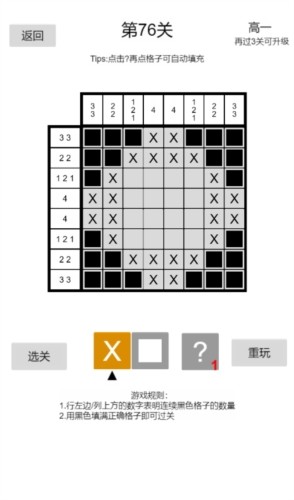
nonogram安卓版描述

1. 創(chuàng)新拼圖體驗(yàn)：nonogram安卓版將數(shù)字推理與藝術(shù)完美結(jié)合，為玩家?guī)砬八从械慕庵i體驗(yàn)。

2. 豐富多樣的關(guān)卡：提供數(shù)百甚至上千個(gè)精心設(shè)計(jì)的關(guān)卡，難度逐漸提升，讓玩家不斷挑戰(zhàn)自我。

3. 精美的圖案收集：完成關(guān)卡后，玩家可以解鎖并收集各種精美的圖案，展示自己的智慧和個(gè)性。

4. 免費(fèi)暢玩無廣告：游戲提供免費(fèi)下載和暢玩，無廣告干擾，確保玩家能夠沉浸在純粹的游戲體驗(yàn)中。